Mathematics In The Neolithic Revolution
Pictured here is the Rhind Mathematical Papyrus. It is one of the earliest preserved examples of mathematics from the ancient world. It was found in the memorial temple of Pharaoh Ramesses II in Luxor Egypt, and it dates back to around 1500 BC, but the original document from which it is copied is likely much older. It contains 87 problems, which are solved using basic algebra and geometry. It contains practical problems such as dividing shares of grain among workers and landlords, calculating the volume of silos and the area of farm plots, and converting between different Egyptian units of measurement. Although today the Papyrus's contents may strike us as mundane, contemporaries viewed them as holding immense power. The scribe copying this page opens by pronouncing that this papyrus gives "Accurate reckoning. The entrance into the knowledge of all existing things and all obscure secrets.”
Background
The Neolithic Revolution, sometimes known as the first agricultural revolution, is one of the most important transitions in all of human history. From a progress studies perspective, it is even more fundamental. The transition to sedentary agricultural life began the cycle of investment into productivity enhancing technologies which is the seed of all progress. Despite this importance, best evidence suggests that anatomically modern humans existed for at least 300 thousand years before successfully starting this cycle.
Productivity enhancing tools are much less appealing to a hunter-gatherer because not only do you have to carry the thing around with you, you also need to carry the extra food that it helps you produce. An improved hunting tool isn’t much good if it weighs ten pounds and you can’t eat the extra gazelle it helps you kill before it rots. Additionally, strict sharing ethics acted as high tax rates for increased food income in hunter-gatherer societies. Taking down more or larger game meant more mouths to feed, so investment in productivity did not translate into individual reward. These societies did develop tools such as the hand-axe and the bow, but these are small and light and they didn’t change much for hundreds of thousands of years after their inception.
The transition to farming brought a number of mutually reinforcing changes. Permanent settlements and farming plots were much easier to demarcate than sprawling hunting grounds. This allowed people to extend ownership beyond the things they carried on their body, so they could build and use heavy technologies. This extension of ownership also strengthened the connection between how much food a person produces and how much they eat, incentivizing productivity improvements. Mathematician and historian Dirk Struik notes that “In comparison with Paleolithic times, the tempo of technical improvement was enormously accelerated. As Neolithic man settled down to primitive farming and semi-permanent dwellings and villages, he developed pottery, carpentry, weaving, baking, brewing; and the smelting of copper and bronze. Invention followed invention: the potter's wheel, the wagon wheel, the hammer, the hoe, tents, huts, rafts, boats.”
If a group of these early humans had figured this out a few thousand years earlier, we might already be amongst the stars. What kept them back so long and what ultimately allowed them to make that leap forward? Answering these questions may give us perspective on our own time and allow us to avoid that horror of future generations lamenting "If only they had started sooner!"
Thus, The Neolithic Revolution was a transition for humanity from a particularly clever species which used tools to adapt to its environment, to a universal-constructor species which adapted its environment to itself. There are many non-mutually exclusive theories of the cause of the transition to agriculture, from physiological, to environmental, to game-theoretic. This post explores the importance of mathematics as a necessary causal factor for the Neolithic Revolution.
The Role of Mathematics
Numeracy is helpful for some aspects of hunter-gatherer life, but it is essential for an agricultural one. Basic notions of size comparison via pairing, the common pattern of languages having words for “one, two, three, many,” and intricate geometry found in paleolithic art show that humans had some mathematical skill even before agriculture.
The mathematical abilities of Neolithic humans advanced in concert with the new requirements of agricultural life. These needs can be summed up into three categories: Surplus, Trade, and Time.
Surplus
Since the sedentary agricultural lifestyle allowed for the creation and storage of large food and livestock surpluses, counting up to arbitrarily high numbers, far beyond the "one, two, three, many" common to hunter-gatherers, was needed. Francis Galton’s account of the Damara, a Bantu hunter-gatherer tribe in East Africa, is illustrative. He reports that their “language only has words for one, two, and three.” despite this “they seldom lose oxen: the way in which they discover the loss of one is not by the number of the herd being diminished, but by the absence of a face they knew." This method was evidently effective enough for their purposes, but it is unsustainable as herds get larger. To keep track of agricultural surpluses, humans needed a more abstract way of looking at numbers. They began by keeping track of the quantities of some objects, like goats or bushels of wheat, by cultivating the same quantity of a different thing which was easier to measure and store, like pebbles or marks in a piece of clay.

This seemingly small step is an important leap in abstract thinking which already begins to reveal the universality of number — 3 sheep, 3 men, and 3 days all share something despite being completely different objects, and the concept of a bijection — pair up each of your goats with a pebble as they leave the barn to graze, and you can pair each pebble with a goat as they return to verify that every goat is there. This connection is deeper than you may think; the Latin word for pebble is calculus.
Humans could not have transitioned to farming without this counting technology. Even if some paleolithic humans with "one, two, three, many" number sense had the idea to sow some seeds that they come back to later, they would have no way to experiment and improve yields. One year may be wetter than another, or they plant seeds in cow dung, or they cultivate symbiotic plants in the same field, but in all these variations the paleolithic farmer produces many stalks of wheat. They have no reliable measurement of output which they can store and compare over time. Farming randomly without mechanisms for improvement is not productive enough to outcompete the hunter-gatherer diet. Therefore, formal counting up to arbitrarily high numbers and storage of this data is a necessary prerequisite for the Neolithic Revolution.
Trade
The counting and abstraction skills which allowed Neolithic humans to keep track of their agricultural surpluses were grown in pursuit of another activity which was newly important for sedentary agriculturalists: Trade.
Simple tally marks or pebble counting works for keeping track of a moderate amount of one quantity, but in the temple economies of Mesopotamian city states that isn't enough. Dozens of people trading dozens of goods in massive quantities obsolesced piles of pebbles and required new innovations.

In particular, this sort of complex trading required the combination of the number concept with ideographic symbols for different types of quantities. It also demanded labor intensive conversions between units, which is what many early instructional texts aim to teach including the Rhind papyrus. If you traded 500 bushels of wheat for 10 hectares of land, what price did you pay per square cubit? And how does it compare to the price that Ibbi-Sin paid for his parcel in Uruk denominated in sheep?
Counterintuitively, mathematics had to be more abstract to answer these practical questions. Numbers became further separated from the fingers and pebbles they had so long been attached to, and fractions expanded beyond the intuitive correspondence between whole numbers and groups of objects.
Without trade, agriculture is not a viable alternative to the hunter-gatherer lifestyle. A self-sufficient farmer probably had to work harder to get less varied nutrition than their hunter-gatherer counterpart. But when that farmer is part of a large group, everyone can specialize in what they do best so overall productivity increases, both in terms of volume and variety. Whether these trading settlements could make more food per-capita than hunter-gatherers in the same area is a question of considerable debate, but more importantly, with trade and specialization they could make a bunch of things that the hunter-gatherers could not. Beautiful painted pottery, woven and colored fabrics, gigantic temples, metal tools, and beer. Without advanced symbolic mathematics, the trade which cemented farming's advantage over hunter-gatherers would not have been possible.
Time
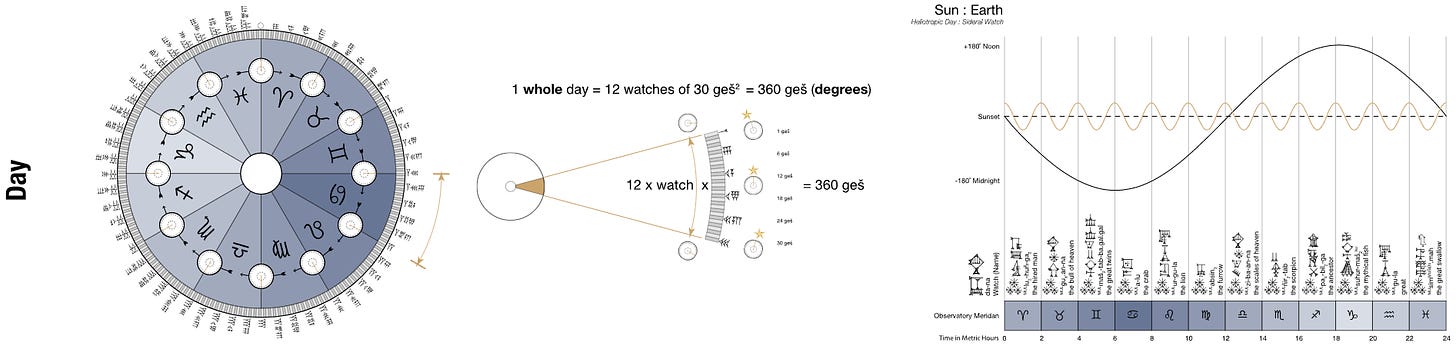
Perhaps the most important motivation for the development of Neolithic mathematics and an unavoidable prerequisite for agriculture is an understanding of time. For Neolithic humans, this was synonymous with understanding the patterns of the celestial bodies which tracked the procession of time on the scale of minutes as the sun transited across the sky each day, on the scale of decades as planetary epicycles and the drift of our galaxy slowly changed the night sky, and everything in-between.
Understanding time is essential for agriculture. A farmer needs to plan out optimal planting and harvesting times at least several months in advance. Time is needed to predict how long a harvest can be stored before rotting, how far a caravan can go before running out of supplies, and for scheduling religious feasts and celebrations. Formalizing the periodicity of the seasons into a calendar is an example of highly abstract mathematical thinking. Our abstractions of time have become so culturally ingrained that it is difficult to imagine thinking of it in any other way, but arranging time onto a single dimension, and tracking it with concentric circles of different periods could not have been obvious to the first humans to think formally about time.
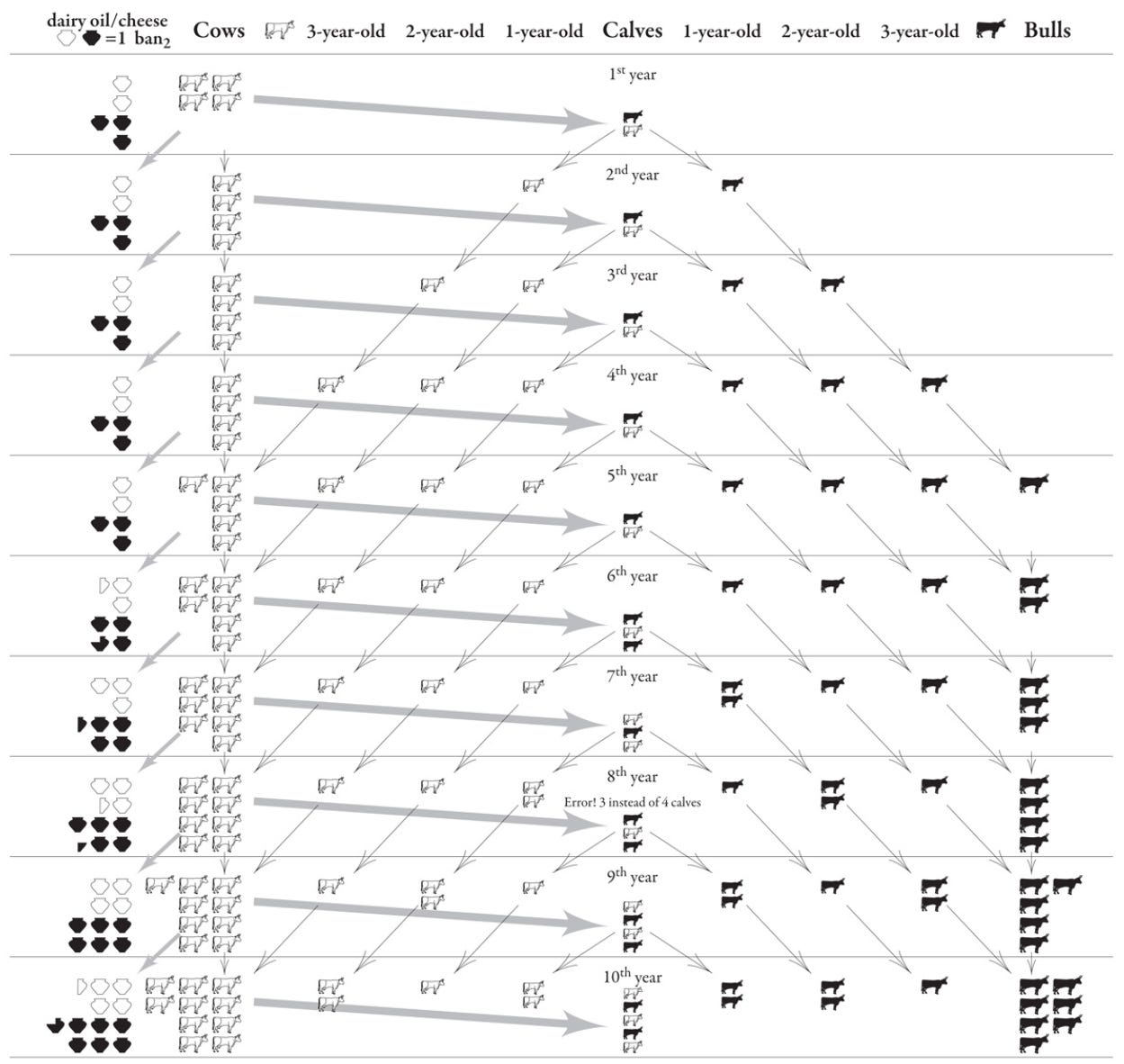
Incredibly, ancient Sumerian farmers were using primitive differential equations to predict the output of their cattle herds several years in advance!
Although the mathematics behind these predictions would not be formalized for thousands of years, they exemplify the importance of time in agriculture. The only way to accomplish the planning and forecasting necessary to build a civilization around agriculture is to deeply understand time. The only way to do that, is by attaching time to the number line, integrating it into equations, and compressing it into abstract symbols.
Conclusion
The Neolithic Revolution is an important milestone in human progress. Mathematics was essential for the Neolithic Revolution. So transitively, mathematics is necessary for human progress.
If the fundamental mathematical ideas that enabled the transition to agriculture had been discovered earlier, our long march up the Kardashev scale could have begun sooner and many years of suffering would be avoided. The best time to discover a fundamental mathematical idea was 300 thousand years ago. The second best time is today. We do not yet know what the next revolution in human organization will be. But we can be confident that mathematics will be an essential ingredient.